Golden Ratio Calculator (φ)

What is φ?
@Reader
The Golden Ratio Formula
The Official Formula
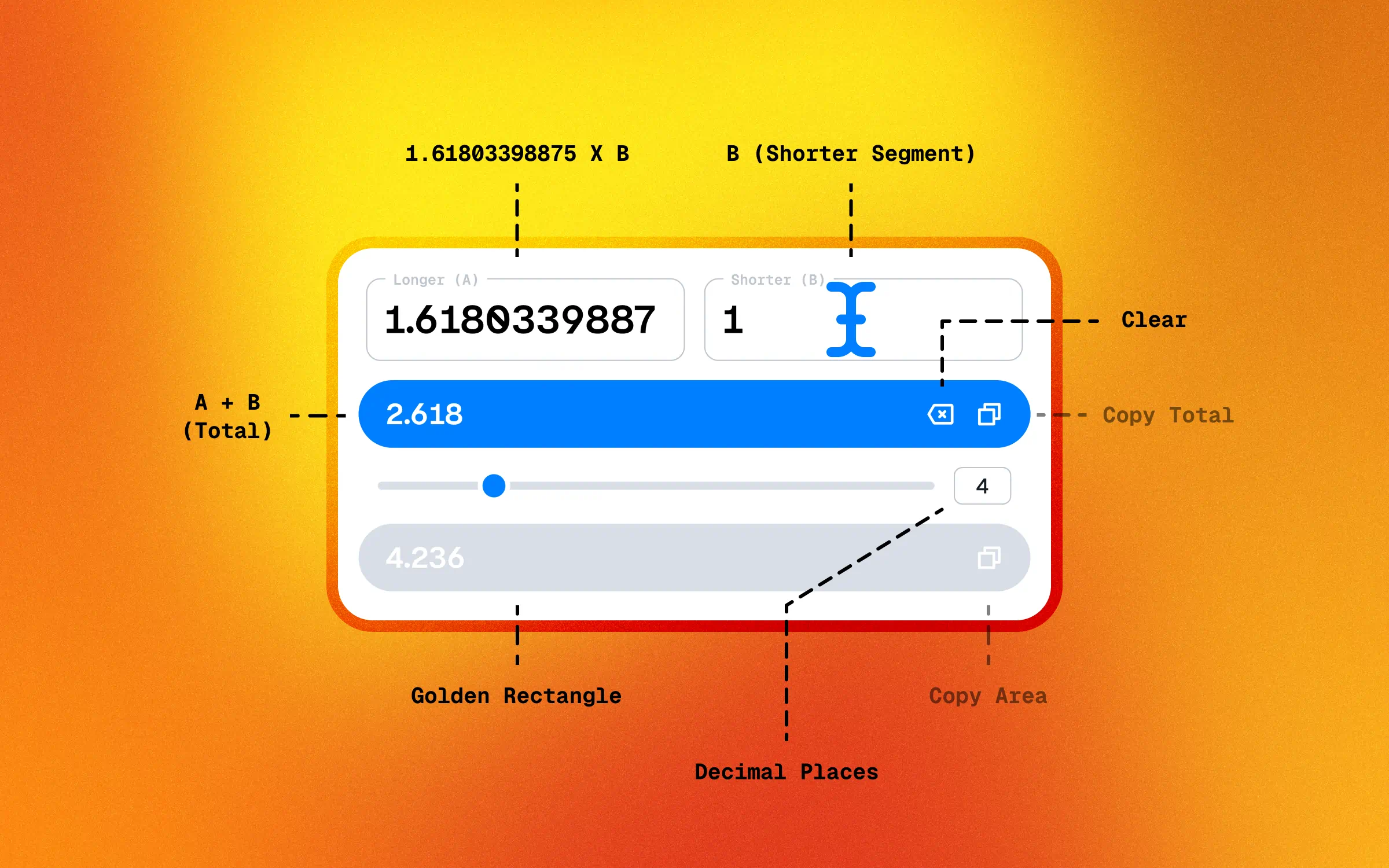
The key characteristic of the golden ratio is that it arises when a line is divided into two parts such that the ratio of the whole length to the longer part is equal to the ratio of the longer part to the shorter part.
a / b = (a + b) / a = φ
(Mathematically, for quantities a and b where a > b > 0).
Why Is the Golden Ratio Important?
The Golden Ratio is a fundamental mathematical concept that appears in various forms of nature, art, and design. It has been used to create balance and harmony in everything from furniture to architecture, and even in finance to analyze stock market patterns and predict future prices.
Here are some cool examples of the Golden Ratio in action:
- The Great Pyramid of Giza’s height-to-base ratio is remarkably close to the Golden Ratio.
- Leonardo da Vinci employed the Golden Ratio to create the Mona Lisa’s perfect facial proportions.
- In music, the Golden Ratio is embedded in the Fibonacci sequence, which is used to craft harmonious melodies.
The golden ratio in nature:
- Spiral arrangement of leaves on a plant, such as a sunflower.
- Ratio of the width to the length of a nautilus shell.
- Hexagonal honeycombs.
- The Human Face.
- Spiral shape of a galaxy.
The Fibonacci Sequence.
The Fibonacci Sequence is a series of numbers where each number is the sum of the previous two. It starts like this: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144… and continues indefinitely. The ratio between each number in the sequence approaches the Golden Ratio (1.618) as the sequence gets larger.
The formula to calculate the nth number in the sequence of Fibonacci numbers is:
Fn = Fn-1 + Fn-2
Where n > 1 and Fn-1 is the (n-1)th Fibonacci number and Fn-2 is the (n-2)th Fibonacci number. The ratio of any two consecutive numbers in the Fibonacci sequence approaches the golden ratio, which is approximately 1.618.