Reverse CAGR Calculator

Estimate the Final Value of an Investment, Based on Compounded Annual Growth Rate.

CAGR = Compounded Annual Growth Rate.

Enter your investment amount, growth rate, and time.

The calculator will instantly show you the maturity value (final value) of your investment.

@Author

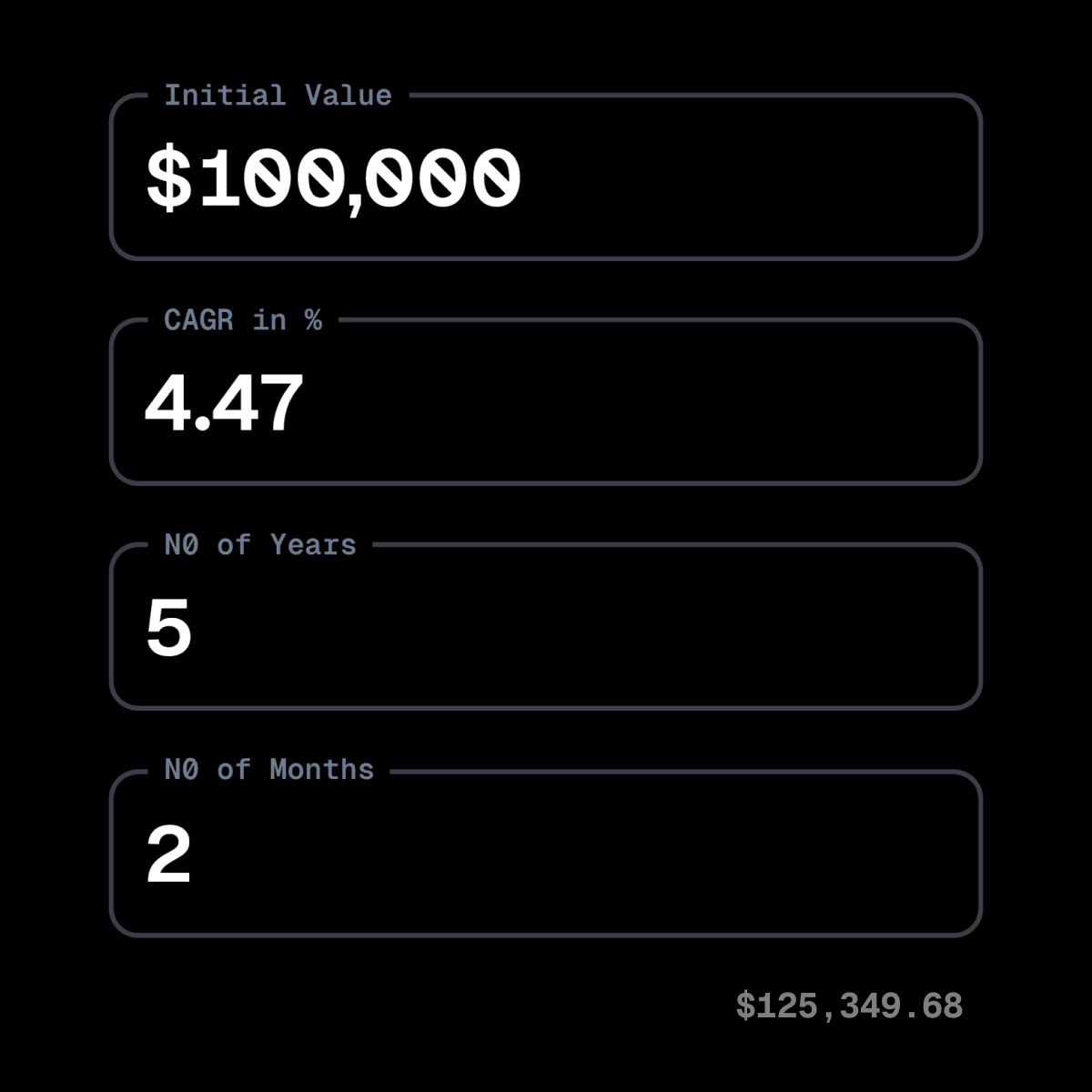
Can I add fractional numbers?

@Reader

Sure, knock yourself out!

Also, you can enter time in years only, months only, or a combination of both.

@Author

What Is Reverse CAGR?

First What Is CAGR?

CAGR is the average rate at which an investment grows each year, over a certain period of time. It considers compounding, which implies that the investment’s gains are reinvested each year to create even higher returns in the future.

(End Value / Start Value)^(1 / Time) - 1

The Reverse CAGR Formula

The reverse CAGR formula is used to calculate the ending value of an investment given the beginning value, the number of years, and the CAGR. The formula is:

Initial * (1 + CAGR) ^ Yrs

Reverse CAGR is a financial metric that is used to calculate the rate at which an investment must grow in order to reach a target value in a specified number of periods. Reverse How Reverse CAGR can help:

Compare investments for better growth.
Find investments that match your goals.
Calculate potential investment returns.
Make informed investment decisions.

The Rule Of 72

The Rule of 72 is a rough estimate of how long it takes for an investment to double in value at a given annual rate of return.

To use it, divide 72 by the annual interest rate.

Example: An 8% annual return means your investment will double in about 9 years (72 ÷ 8 = 9).